Префиксное дерево

Префиксное дерево или бор (англ. trie) — структура данных для компактного хранения строк, устроенная в виде дерева, где на рёбрах между вершинами записаны символы, а некоторые вершины помечены терминальными.

Говорят, что префиксное дерево принимает строку $s$, если существует такая терминальная вершина $v$, что, если выписать подряд все буквы на путях от корня до $v$, то получится строка $s$.

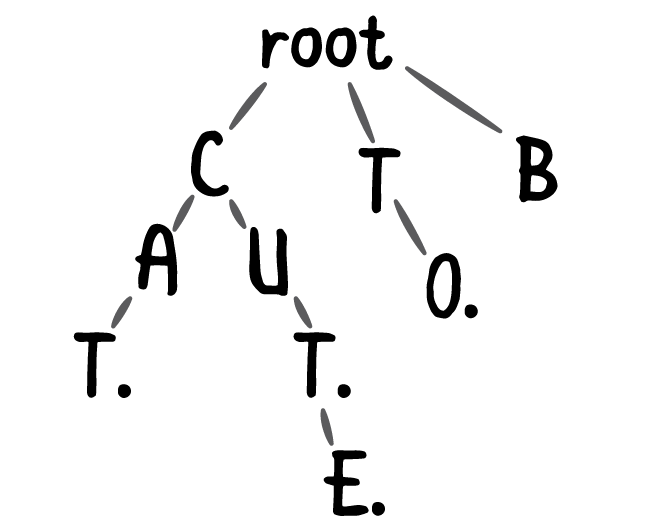
Бор сам по себе можно использовать для разных задач:

• Хранение строк: если есть много повторяющихся длинных префиксов, то бор может занимать гораздо меньше места, чем массив или set строк.
• Сортировка строк: по построенному бору можно пройтись dfs-ом и вывести все строки в лексикографическом порядке.
• Просто как множество строк: как мы увидим, в бор легко добавлять и удалять слова, а также делать проверки вхождения.

С точки зрения теории автоматов, каждая вершина — это состояние, а все корректные односимвольные дополнения являются корректными переходами в автомате. Бор таким образом является автоматом, проверяющим вхождение слова в множество.

#Реализация

Префиксное дерево проще всего хранить в виде ссылающихся друг на друга вершин. В каждой вершине обычно хранится, является ли вершина терминальной, ссылки на детей, и какая дополнительная информация, зависящая от задачи — например, если мы хотим реализовать мультисет, можно хранить количество слов, заканчивающихся в вершине.

Для латинского алфавита (в котором 26 строчных букв) изначально пустой бор можно реализовать так:

const int k = 26;

struct Vertex {
    Vertex* to[k] = {0}; // нулевой указатель означает, что перехода нет
    bool terminal = 0;
};

Vertex *root = new Vertex();

Чтобы добавить слово в бор, нужно пройтись от корня по символам слова. Если перехода по для очередного символа нет — создать его, иначе пройти по уже существующему. В конце текущее состояние нужно не забыть пометить терминальным.

void add_string(string &s) {
    v = root;
    for (char c : s) {
        c -= 'a'; // получаем число от 0 до 25
        if (!v->to[c]) 
            v->to[c] = new Vertex();
        v = v->to[c];
    }
    v->terminal = true;
}

Чтобы проверить, есть ли слово в боре, нужно так же пройти от корня по символам слова. Если в конце оказались в терминальной вершине — то слово есть. Если оказались в нетерминальной вершине или когда-нибудь потребовалось пройтись по несуществующей ссылке — то нет.

bool find(string &s) {
    v = root;
    for (char c : s) {
        c -= 'a';
        if (!v->to[c])
            return false;
        v = v->to[c];
    }
    return v->terminal;
}

Удалить слово можно «лениво»: просто дойти до него и убрать флаг терминальности.

bool erase(string &s) {
    v = root;
    for (char c : s)
        v = v->to[c - 'a'];
    v->terminal = false;
}

В зависимости от задачи эти процедуры иногда следует изменить. Например, если мы хотим реализовать автодополнение — по запросу найти все слова с заданным префиксом — можно аккуратно удалять вершины, если они не ведут в терминальные вершины, и тогда при ответе на запрос можно просто пройтись dfs-ом из состояния-префикса, выводя ответ во всех терминальных вершинах.

#Как хранить ссылки

Иногда ограничения не позволяют хранить ссылки на детей просто в массиве.

Например, если алфавит большой — тогда нам не хватит ни времени, ни памяти инициализировать столько массивов, большинство из которых будут пустыми.

Помимо массивов указателей, есть много других способов хранить отображение из символа в ссылку:

• расширяющийся массив (std::vector),
• бинарное дерево (std::map),
• хеш-таблица (std::unordered_map).

Чаще всего память является основным практическим соображением. Также на 64-битных системах может быть выгодно вместо new и указателей выделять всё на большом массиве или векторе и хранить 4-байтные индексы вершин вместо 8-байтных указателей на память.

#Цифровой бор

В некоторых задачах появляется идея хранить в боре числа, подобно строкам — такая структура называется цифровым бором.

Чаще всего числа надо записывать в двоичной системе счисления, и тогда все очень просто, но в некоторых задачах требуется какая-то другая система счисления, а так, например, как сравнивать числа в лексикографическом порядке в десятичной системе счисления нельзя (2 > 11). Чтобы избавиться от этого момента, будем считать, что все числа меньше какой-то степени 10, и тогда будем просто дополнять число ведущими нулями: теперь 02 < 11.

Задача. Задано некоторое множество чисел, и требуется отвечать на три вида запросов:

1. Добавить число $x$.
2. Удалить число $x$.
3. Найти число $y$ в массиве, у которого xor c $x$ максимален.

Первые два вида запросов мы уже умеем делать в цифровом боре, а запрос третьего типа сложнее.

Заметим, что если существует $y$ из множества, такой что $y_i \neq x_i$ (то есть они отличаются в $i$-ом бите), то взять его выгоднее, чем любое другое число, у которого префикс до $i$-того бита включительно равен префиксу $x$ — потому что xor такого числа с $x$ будет содержать только меньшие биты, чем $i$-тый, и соответственно не будет превосходить $2^i$, который мы уже можем получить с $y$.

Тогда при ответе на запрос третьего типа мы можем жадно спускаться по бору, каждый раз пытаясь пойти в ветку, у которой $i$-тый бит не равен $x_i$.