Единственные требования, накладываемые на функцию $f$ — что у неё есть хотя бы один корень и что она непрерывна и дифференцируема на интервале поиска.
#Описание алгоритма
Алгоритм начинает с какого-то изначального приближения $x_0$ и затем итеративно строит лучшее решение, строя касательную к графику в точке $x = x_i$ и присваивая в качестве следующего приближения $x_{i+1}$ координату пересечения касательной с осью $x$. Интуиция в том, что если функция $f$ «хорошая», и $x_i$ уже достаточно близок к корню, то $x_{i+1}$ будет ещё ближе.
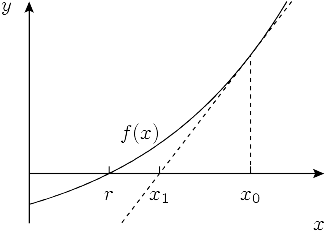
Чтобы получить точку пересечения для $x_i$, нужно приравнять уравнение касательной к нулю:
$$ 0 = f(x_i) + (x_{i+1} - x_i) f'(x_i) $$ откуда можно выразить $$ x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)} $$Метод Ньютона крайне важен в вычислительной математике: в большинстве случаев именно он используется для нахождения численных решений уравнений.
#Поиск квадратных корней
В качестве конкретного примера рассмотрим задачу нахождения квадратных корней, которую можно переформулировать как решение следующего уравнения:
$$ x = \sqrt n \iff x^2 = n \iff f(x) = x^2 - n = 0 $$ Если в методе Ньютона подставим $f(x) = x^2 - n$, мы получим следующее правило: $$ x_{i+1} = x_i - \frac{x_i^2 - n}{2 x_i} = \frac{x_i + n / x_i}{2} $$Если нам нужно посчитать корень с некоторой заданной точностью $\epsilon$, можно на каждой итерации делать соответствующую проверку:
const double eps = 1e-9;
double sqrt(double n) {
double x = 1;
while (abs(x * x - n) > eps)
x = (x + n / x) / 2;
return x;
}
Алгоритм успешно сходится к правильному ответу для многих функций, однако это происходит надежно и доказуемо только для определенного множества функций (например, выпуклых). Другой вопрос — как быстра эта сходимость, если она происходит.
#Скорость сходимости
Запустим метод Ньютона для поиска квадратного корня $2$, начиная с $x_0 = 1$, и посмотрим, сколько первых цифр оказались правильными после каждой итерации:
1.0000000000000000000000000000000000000000000000000000000000000 1.5000000000000000000000000000000000000000000000000000000000000 1.4166666666666666666666666666666666666666666666666666666666675 1.4142156862745098039215686274509803921568627450980392156862745 1.4142135623746899106262955788901349101165596221157440445849057 1.4142135623730950488016896235025302436149819257761974284982890 1.4142135623730950488016887242096980785696718753772340015610125 1.4142135623730950488016887242096980785696718753769480731766796
Можно заметить, что число корректных цифр примерно удваивается после каждой итерации. Такая прекрасная скорость сходимости не просто совпадение.
Чтобы оценить скорость сходимости численно, рассмотрим небольшую относительную ошибку $\delta_i$ на $i$-ой итерации и посмотрим, насколько меньше станет ошибка $\delta_{i+1}$ на следующей итерации.
$$ |\delta_i| = \frac{|x_n - x|}{x} $$ В терминах относительных ошибок, мы можем выразить $x_i$ как $x \cdot (1 + \delta_i)$. Подставляя это выражение в формулу для следующей итерации и деля обе стороны на $x$ получаем $$ 1 + \delta_{i+1} = \frac{1}{2} (1 + \delta_i + \frac{1}{1 + \delta_i}) = \frac{1}{2} (1 + \delta_i + 1 - \delta_i + \delta_i^2 + o(\delta_i^2)) = 1 + \frac{\delta_i^2}{2} + o(\delta_i^2) $$Здесь мы разложили $(1 + \delta_i)^{-1}$ в ряд Тейлора в точке $0$, используя предположение что ошибка $d_i$ мала: так как последовательность $x_i$ сходится к $x$, то $d_i \ll 1$ для достаточно больших $n$.
Наконец, выражая $\delta_{i+1}$, получаем
$$ \delta_{i+1} = \frac{\delta_i^2}{2} + o(\delta_i^2) $$что означает, что относительная ошибка примерно возводится в квадрат и делится пополам на каждой итерации, когда мы уже близки к решению. Так как логарифм $(- \log_{10} \delta_i)$ примерно равен числу правильных значимых цифр числа $x_i$, возведение ошибки в квадрат соответствует удвоению значимых цифр ответа, что мы и наблюдали ранее.
Это свойство называется квадратичной сходимостью, и оно относится не только к нахождению квадратных корней. Оставляя формальное доказательство в качестве упражнения, можно показать, что в общем случае
$$ |\delta_{i+1}| = \frac{|f''(x_i)|}{2 \cdot |f'(x_n)|} \cdot \delta_i^2 $$ что означает хотя бы квадратичную сходимость при нескольких дополнительных предположениях, а именно что $f’(x)$ не равна нулю и $f’’(x)$ непрерывна.