Ро-алгоритм Полларда — рандомизированный алгоритм факторизации целых чисел, работающий за время $O(n^\frac{1}{4})$ и основывающийся на следствии из парадокса дней рождений:
В мультимножество нужно добавить $O(\sqrt{n})$ случайных чисел от 1 до $n$, чтобы какие-то два совпали.
#$\rho$-алгоритм Полларда
Итак, мы хотим факторизовать число $n$. Предположим, что $n = p q$ и $p \approx q$. Понятно, что труднее случая, наверное, нет. Алгоритм итеративно ищет наименьший делитель и таким образом сводит задачу к как минимум в два раза меньшей.
Возьмём следующую функцию:
$$ f(x) = (x+1)^2 \bmod n $$Одно из свойств, которое нам понадобится в алгоритме, заключается в том, что эта функция «достаточно случайная» с точки зрения теории чисел. Мы к этой функции ещё вернемся.
Определение. Граф, в котором из каждой вершины есть единственное ребро $x \to f(x)$, называется функциональным.
Если в функциональном графе нарисовать «траекторию» произвольного элемента, то получится какой-то путь, превращающийся в цикл.
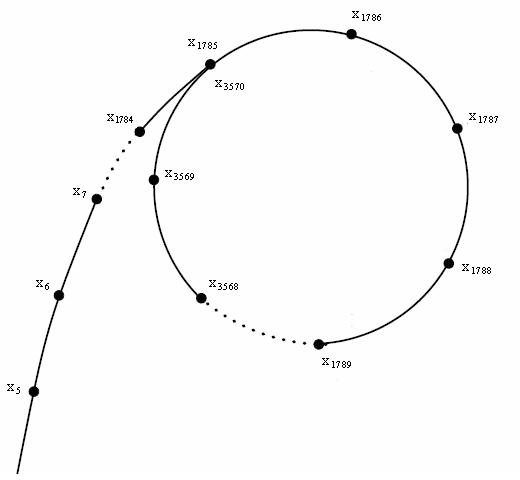
Рассмотрим траекторию какого-нибудь элемента $x_0$: {$x_0$, $f(x_0)$, $f(f(x_0))$, $\ldots$}. Сделаем из неё новую последовательность, мысленно взяв каждый элемент по модулю $p$ — меньшего из простых делителей $n$.
Утверждение. Ожидаемая длина цикла в этой последовательности $O(\sqrt[4]{n})$.
Доказательство: так как $p$ — меньший делитель, то $p \leq \sqrt n$. Теперь просто подставим в следствие из парадокса дней рождений: в множество нужно добавить $O(\sqrt{p}) = O(\sqrt[4]{n})$ элементов, чтобы какие-то два совпали, а значит последовательность зациклилась.
Если мы найдём цикл в такой последовательности, то есть такие $i$ и $j$, что
$$ f^i(x_0) \equiv f^j(x_0) \pmod p $$ то мы сможем найти и какой-то делитель $n$, а именно $$ d = \gcd(|f^i(x_0) - f^j(x_0)|, n) $$Это число меньше $n$ и делится на $p$, а значит должно быть равно ему.
Алгоритм по сути находит цикл в этой последовательности, используя для этого стандартный алгоритм «черепаха и заяц»: будем поддерживать два удаляющихся друг от друга указателя $j$ и $i = 2j$ и проверять, что $f^i(x_0) \equiv f^j(x_0)$, что эквивалентно проверке
$$ \gcd(|f^i(x_0) - f^j(x_0)|, n) \not \in \{ 1, n \} $$Простая, но не самая надежная реализация:
typedef long long ll;
inline ll f(ll x, ll n) { return (__int128_t) (x + 1) * (x + 1) % n; }
ll find_divisor(ll n, ll seed = 1) {
ll x = seed, y = seed;
ll d = 1;
while (d == 1 || d == n) {
// двигаем первый указатель на шаг
y = f(y);
// а второй -- на два
x = f(f(x));
// пытаемся найти общий делитель
d = gcd(abs(x - y), n);
}
return d;
}
Так как алгоритм рандомизированный, при полной реализации нужно учитывать разные детали. Например, что иногда делитель не находится (нужно запускать несколько раз), или что при попытке факторизовать простое число он будет работать за $O(\sqrt n)$ (нужно добавить тест на простоту или отсечение по времени).
Асимптотика этой реализации будет $O(\sqrt[4]{n} \log n)$, потому что мы на каждой итерации ищем $\gcd$ за $O(\log n)$. От логарифма можно избавиться следующим трюком: объявим константу $M = \Theta(\log n)$ и будем поддерживать произведение значений $P = \prod |f^i(x_0) - f^j(x_0)|$ по модулю $n$ для $M$ последовательных итераций, и, вместо проверок через подсчет $\gcd$ на каждом шаге, будем каждые $M$ итераций считать $\gcd(P, n)$.
Когда мы дойдем до делителя, он будет учтен в произведении, и мы не более чем через $M = \Theta(\log n)$ шагов найдем его в $\gcd$ произведения. Так как мы теперь лишь каждые $\Theta(\log n)$ считаем $\gcd$ за $O(\log n)$, то логарифм из асимптотики исчезнет.
#Примечания
Факторизация больших чисел интересна в контексте криптографии — на предположение невозможности факторизации за линейное время опирается, например, алгоритм RSA.
Существуют также субэкспоненциальные, но не полиномиальные алгоритмы факторизации. Человечество умеет факторизовывать числа порядка $10^{250}$.
Алгоритм Шора позволяет факторизовывать числа за полиномиальное время на квантовом компьютере. Но на 2019 год все квантовые вычисления проще симулировать на обычном компьютере. Самое большое число, факторизованное на реальном квантовом компьютере — 4088459.