Как уже упоминалось ранее, иногда существенную роль играет то, что алгоритм Джарвиса работает за $O(nh)$, а не $O(n^2)$: когда известно, что оболочка небольшая, он лучше алгоритма Грэхэма за $O(n \log n)$.
Алгоритм Чана пытается получить лучшее из двух и объединить алгоритмы Джарвиса и Грэхэма, чтобы получить асимптотику $O(n \log h)$.
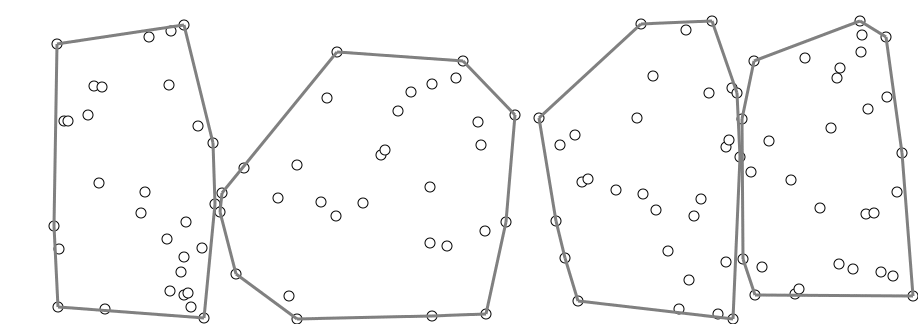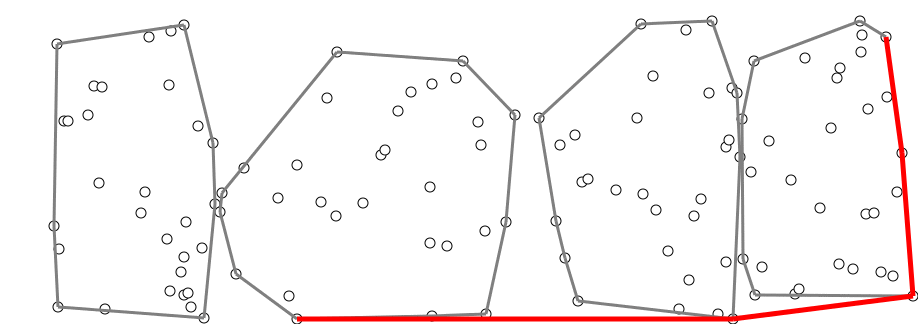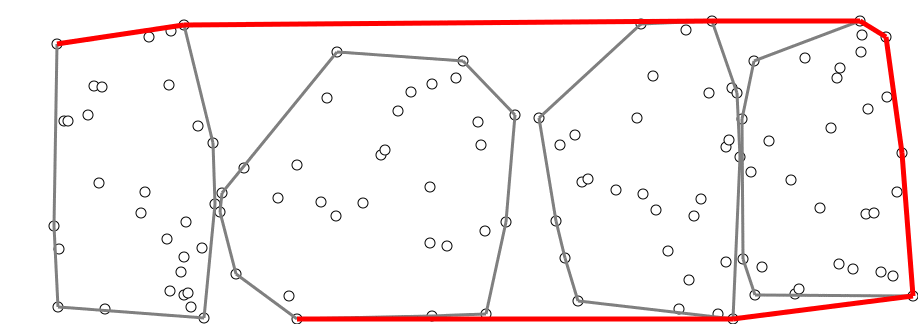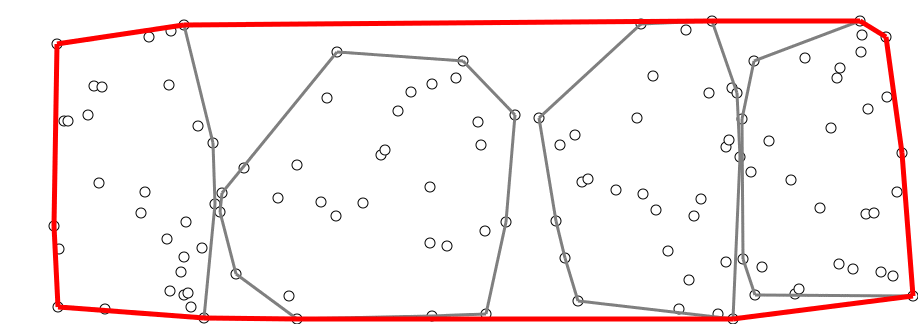
Алгоритм. Разделим все точки на группы по $m$ точек. В каждой группе построим выпуклую оболочку за $O(m \log m)$ алгоритмом Грэхэма. Точки никак не упорядочены, и эти оболочки могут пересекаться — это нормально. Суммарно для всех групп понадобится $O(n \log m)$ операций.
Затем, начиная с самой левой нижней точки, мы будем строить общую выпуклую оболочку аналогично алгоритму Джарвиса, но теперь «самую правую точку» можно находить каждый раз не за $O(n)$, а за $O(\frac{n}{m} \log m)$, если делать бинарный поиск в каждой из $\frac{n}{m}$ оболочек.
Получается, что такое решение будет работать за $O(h \frac{n}{m} \log m + n \log m)$. Если заранее приблизительно знать $h$, то можно положить $m = h$, и тогда асимптотика составит $O(n \log h)$.
Понятно, что ни при каких применимых на практике ограничениях, даже если оболочка состоит из трёх точек, этот алгоритм не будет быстрее обычного алгоритма Грэхэма, так что автор не будет приводить его реализацию. Этот способ просто интересен с теоретической точки зрения.
Упражнение. Придумайте, как при неизвестном $h$ подбирать $m$ так, чтобы асимптотика оставалась $O(n \log h)$.