Экстраполяцией называется построение математических моделей, предсказывающих значения вне некоторого известного промежутка — например, следующее значение по известным предыдущим.
Интерполяцией же называется приближенное нахождение промежуточных значений между известными.
В более узком смысле, в контексте алгебры, интерполяцией называется нахождение многочлена, проходящего через заданный набор точек $(x_i, y_i)$.
#Интерполяционный многочлен Лагранжа
Теорема. Пусть есть набор различных точек $x_0, x_1, \dots, x_{n}$. Многочлен степени $n$ однозначно задаётся своими значениями в этих точках.
Примечание: коэффициентов у этого многочлена столько же, сколько и точек.
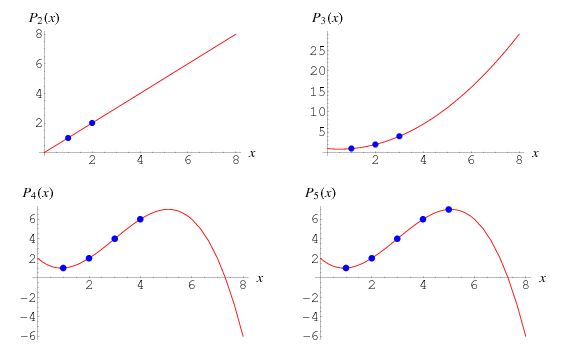
Доказательство будет конструктивным — можно явным образом задать многочлен, который принимает заданные значения $y_0, y_1, \ldots, y_n$ в этих точках:
$$ y(x)=\sum\limits_{i=0}^{n}y_i\prod\limits_{j\neq i}\dfrac{x-x_j}{x_i-x_j} $$Этот многочлен называется интерполяционным многочленом Лагранжа.
Корректность. Проверим, что в точке $x_i$ значение действительно будет равно $y$:
Для $i$-го слагаемого внутреннее произведение будет равно единице, если вместо $x$ подставить $x_i$: в этом случае просто перемножается $(n-1)$ единица. Эта единица помножится на $y_i$ и войдёт в сумму.
Для всех остальных слагаемых произведение занулится: один из множителей будет равен $(x_i - x_i)$.
Уникальность. Предположим, есть два подходящих многочлена степени $n$: $A(x)$ и $B(x)$. Рассмотрим их разность. В точках $x_i$ значение получившегося многочлена $A(x) - B(x)$ будет равняться нулю. Если так, то точки $x_i$ должны являться его корнями, и тогда разность можно записать так:
$$ A(x) - B(x) = \alpha \prod_{i=0}^n (x-x_i) $$для какого-то числа $\alpha$. Тут мы получаем противоречие: если раскрыть это произведение, то получится многочлен степени $n+1$, который нельзя получить разностью двух многочленов степени $n$.
#Интерполяция на практике
Примечание. На практике интерполяцию решают методом Гаусса: её можно свести к решению линейного уравнения $aX = y$, где $X$ это матрица следующего вида:
$$ \begin{pmatrix} 1 & x_0 & x_0^2 & \ldots & x_0^n \\ 1 & x_1 & x_1^2 & \ldots & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \ldots & x_n^n \\ \end{pmatrix} $$Важный факт — многочлен степени $n$ можно однозначно задать
- своими $(n+1)$ коэффициентами,
- значениями хотя бы в $(n + 1)$ точке,
- своими $n$ корнями (возможно, комплексными и дублирующимися) и коэффициентом $\alpha$: