Эйлеров цикл

Определение. Эйлеров путь — это путь в графе, проходящий через все его рёбра.

Определение. Эйлеров цикл — это эйлеров путь, являющийся циклом.

Для простоты в обоих случаях будем считать, что граф неориентированный.

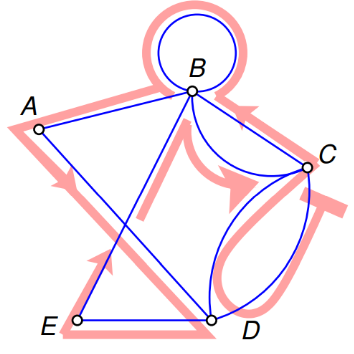
Также существует понятие гамильтонова пути и цикла — они посещают все вершины по разу, а не рёбра. Нахождение гамильтонова цикла (задача коммивояжера, англ. travelling salesman problem) — одна из самых известных NP-полных задач, в то время как нахождение эйлерова цика решается за линейное время, и мы сейчас покажем, как.

#Нахождение эйлерова цикла

Теорема. Эйлеров цикл существует тогда и только тогда, когда граф связный и степени всех вершин чётны.

Доказательство. Необходимость показывается так: можно просто взять эйлеров цикл и ориентировать все его ребра в порядке обхода. Тогда из каждой вершины будет выходить столько же рёбер, сколько входить, а значит степень у всех вершин исходного неориентированного графа была четной.

Достаточность докажем конструктивно — предъявим алгоритм нахождения цикла:

void euler(int v) {
    while (!g[v].empty()) {
        u = *g[v].begin(); // берем любое ребро
        remove_edge(v, u); // удаляем его
        euler(u);            // запускаемся от противоположного конца
    }
    cout << v <<  " ";     // выписываем текущую вершину
}

Заметим, что:

• выведется последовательность из ровно $(m + 1)$ вершин,
• между каждой соседней парой выписанных вершин есть ребро,
• каждое ребро будет выписано ровно один раз.

Значит, если условия на связность и четность степеней выполняются, то выведенная последовательность вершин действительно будет эйлеровым циклом, причём и в случае ориентированного графа тоже.

#Как удалять ребра

Проще всего хранить все списки смежности в set-подобной структуре и удалять их напрямую там:

const int maxn = 1e5;
set<int> g[maxn];

void euler(int v) {
    while (!g[v].empty()) {
        u = *g[v].begin();
        g[v].erase(u);
        g[u].erase(v); // если граф ориентированный, обратное ребро удалять не надо
        euler(u);
    }
    cout << v <<  " ";
}

Это будет работать за $O(m \log n)$, однако просто заменив дерево на хеш-таблицу (unordered_set) можно уменьшить время до линейного.

Также можно использовать более общий подход, который часто применяется в задачах, где ребра как-то изменяются. Создадим отдельный массив с мета-информацией о ребрах и будем хранить в списках смежности не номера вершин, а номера рёбер:

struct edge {
    int to;
    bool deleted;
};

vector<edge> edges;
stack<int> g[maxn];

void add_edge(int u, int v) {
    g[u].push(edges.size());
    edges.add({v, false});
    g[u].push(edges.size());
    edges.add({u, false});
}

Если добавлять каждое ребро неориентированного графа через add_edge, то у получившейся нумерации ребер будет интересное свойство: чтобы получить обратное к ребру e, нужно вычислить e^1.

Тогда во время обхода можно поддерживать эту информацию вместо какой-то сложной модификации структур:

void euler(int v) {
    while (!g[v].empty()) {
        e = g[v].top();
        g[v].pop();
        if (!edges[e].deleted) {
            edges[e].deleted = edges[e^1].deleted = true;
            euler(e.to);
        }
    }
    cout << v <<  " ";
}

Во всех вариантах реализации нужно быть чуть аккуратнее в случае, когда в графе есть петли и кратные ребра.

#Эйлеров путь

Поговорим теперь про эйлеровы пути. Может, всё-таки можно что-нибудь сделать, даже если степени не всех вершин чётные?

Заметим, что, так как каждое ребро меняет четность степеней ровно двух вершин, и в пустом графе все степени изначально нулевые, то число вершин с нечетными степенями будет четным.

Если нечетных вершин ровно две, то можно сделать следующее: соединить их ребром, построить эйлеров цикл (ведь теперь степени всех вершин четные), а затем удалить это ребро из цикла. Если правильно сдвинуть этот цикл, мы получили эйлеров путь.

Альтернативно, можно просто запустить обход из одной из нечетных вершин и получить такой же результат.

Если нечетных вершин больше двух, то мы уже построить эйлеров путь не сможем, потому что любой эйлеров путь входит или покидает каждую вершину четное число раз, кроме, возможно двух своих концов.

Следствие. Эйлеров путь существует тогда и только тогда, когда граф связен и количество вершин с нечётными степенями не превосходит 2.

Упражнение. Дан связный неориентированный граф. Требуется покрыть его ребра наименьшим количеством непересекающихся путей. Асимптотика $O(n + m)$.

Упражнение. Сформулируйте и докажите аналогичные утверждения для случая ориентированного графа.