Рандомизированные алгоритмы делятся на две категории, названные в честь известных игорных центров:
- Алгоритмы Лас-Вегас гарантированно находят правильный ответ, но требуют недетерминированное количество времени для работы. Например, Quicksort является таким алгоритмом.
- Алгоритмы Монте-Карло требуют детерминированное время для работы, но с какой-то вероятностью могут дать неправильный ответ. Например, тестирование на простоту почти всегда подразумевает какую-то вероятность ошибки.
В контексте численных методов, алгоритмы Монте-Карло часто используются для подсчета некоторых величин, где высокая точность не нужна.
#Подсчет площадей
Рассмотрим следующую задачу. Дана карта города (для простоты, предположим, что это единичный квадрат) и список координат сотовых вышек и их радиусов действия. Требуется посчитать площадь покрытия в этом городе, то есть доля точек города, имеющих хотя бы одну вышку в пределах радиуса её действия
Можно перефразировать эту задачу как нахождение площади пересечения единичного квадрата и объединения кругов. Эта задача имеет точное, но очень сложное решение, которое требует подсчета всех «точек интереса» где какие-либо две фигуры пересекаются, прохождения по ним сканирующей прямой и подсчета кучи нетривиальных интегралов на каждом свободном от пересечений отрезке. Это решение настолько точное, насколько позволяет действительнозначная арифметика, однако медленное и очень неприятное в реализации для не-экспертов в вычислительной геометрии.
Вместо всего этого можно поступить следующим образом: взять несколько случайных точек на квадрате и для каждой из них независимо проверить, покрыта ли она каким-нибудь кругом с помощью простого предиката:
Тогда доля покрытых точек будет нашей оценкой ответа, и если мы взяли достаточно точек, то эта оценка будет близка к реальности.
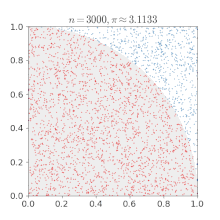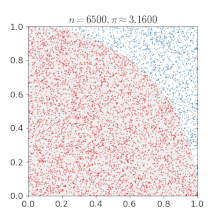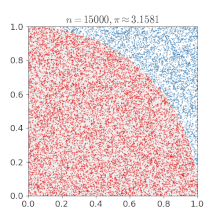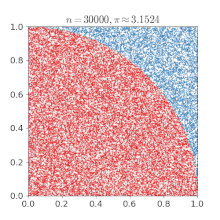
Если у нас есть какое-то формальное требование точности нашего ответа — например, если нам нужно получить 3 правильных значимых знака хотя бы 99% времени — как много точек нам нужно проверить?
Можно показать, что, чтобы получить правильных знаков с произвольно близкой к единице вероятностью, потребуется точек.
Для доказательства этого факта читатель перенаправляется в раздел теорвера.