Алгоритм имитации отжига (англ. simulated annealing) — эвристический алгоритм глобальной оптимизации, особенно эффективный при решении дискретных и комбинаторных задач.
Алгоритм вдохновлён процессом отжига в металлургии — техники, заключающейся в нагревании и постепенном охлаждении металла для увеличения его кристаллизованности и уменьшения дефектов. Симулирование отжига в переборных задачах может быть использовано для приближённого нахождения глобального минимума функций с большим количеством свободных переменных.
Алгоритм вероятностный и не даёт почти никаких гарантий сходимости, однако хорошо работает на практике при решении NP-полных задач. Иногда на контестах им удаётся сдать сложные комбинаторные задачи, у которых есть нормальное решение: например, Ильдар Гайнуллин как-то раз в 8-м классе сдал отжигом div2E на динамику по подмножествам.
#Общее описание алгоритма
Для конкретного примера будем рассматривать задачу коммивояжёра:
Есть $n$ городов, соединённых между собой дорогами. Необходимо проложить между ними кратчайший замкнутый маршрут, проходящий через каждый город только один раз.
Пусть имеется некоторая функция $f(x)$ от состояния $x$, которую мы хотим минимизировать. В данном случае $x$ это перестановка вершин (городов) в том порядке, в котором мы будем их посещать, а $f(x)$ это длина соответствующего пути.
Возьмём в качестве базового решения какое-то состояние $x_0$ и будем пытаться его улучшать. В нашем примере мы можем взять случайную перестановку как изначальный маршрут.
Введём температуру $t$ — какое-то действительное число, изначально равное единице, которое будет изменяться в течение оптимизации и влиять на вероятность перейти в соседнее состояние.
Пока не придём к оптимальному решению или пока не закончится время, будем повторять следующие шаги:
- Уменьшим температуру $t_{k} = T(t_{k-1})$ по какой-то формуле $T$.
- Выберем случайного соседа $x$: какое-то состояние $y$, которое может быть получено из $x$ каким-то небольшим изменением.
- С вероятностью $p(f(x), f(y), t_k)$ сделаем присвоение $x \leftarrow y$, иначе оставим $x$ как есть.
В каждом шаге есть много свободы при реализации. Основные эвристические соображения следующие:
В начале оптимизации наше решение и так плохое, и мы можем позволить себе высокую температуру и риск перейти в состояние хуже. В конце наоборот — наше решение почти оптимальное, и мы не хотим терять прогресс. Температура должна быть высокой в начале и медленно уменьшаться к концу.
Алгоритм будет работать лучше, если функция $f(x)$ «гладкая» относительно этого изменения, то есть изменяется не сильно.
Вероятность должна быть меньше, если новое состояние хуже, чем старое. Также вероятность должна быть больше при высокой температуре.
Например, в коммивояжере можно действовать так:
$t_k = \gamma \cdot t_{k-1}$, где $\gamma$ это какое-то число, близкое к единице (например, $0.99$). Оно должно зависеть от планируемого количества итераций: оптимизация при низкой температуре почти ничего не будет менять.
В случае с перестановками этим минимальным изменением может быть, например, своп двух случайных элементов.
Если $y$ не хуже, то есть $f(y) \leq f(x)$, то переходим в него в любом случае. Иначе делаем переход в $y$, с вероятностью $p = e^\frac{f(x)-f(y)}{t_k}$ — это экспонента отрицательного числа, и она даст вероятность в промежутке $(0, 1)$.
Но важно осознавать, что в выборе конкретных эвристик не существует «золотого правила»: все компоненты алгоритма сильно зависят друг от друга и от задачи.
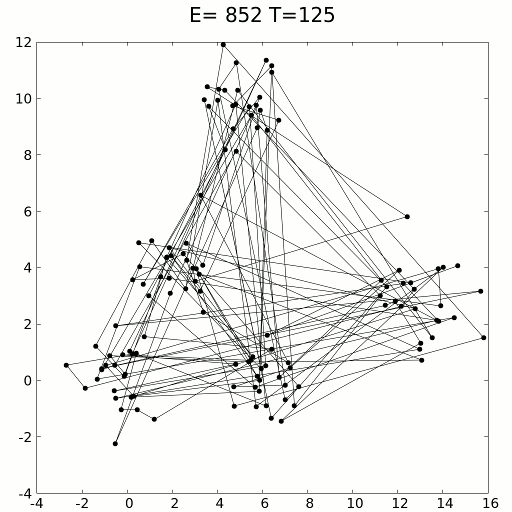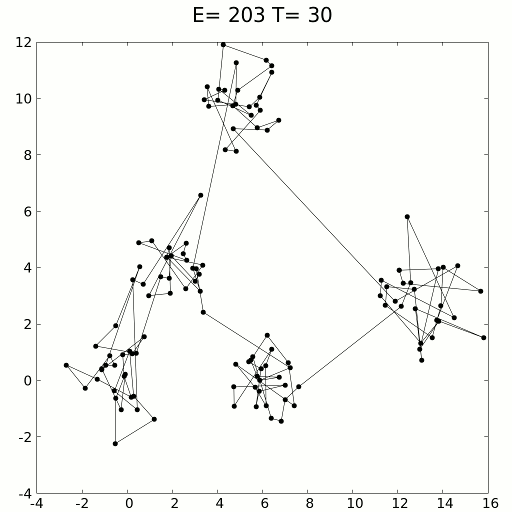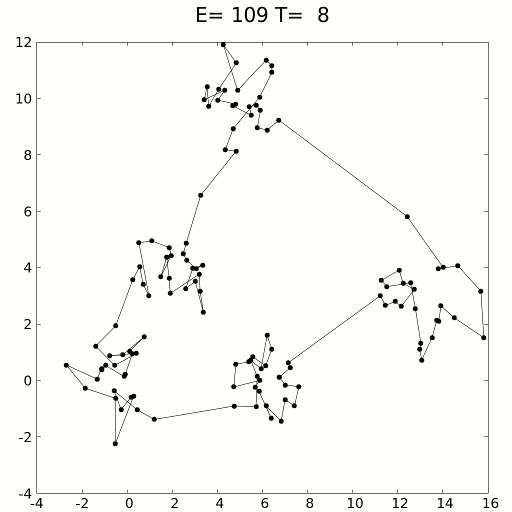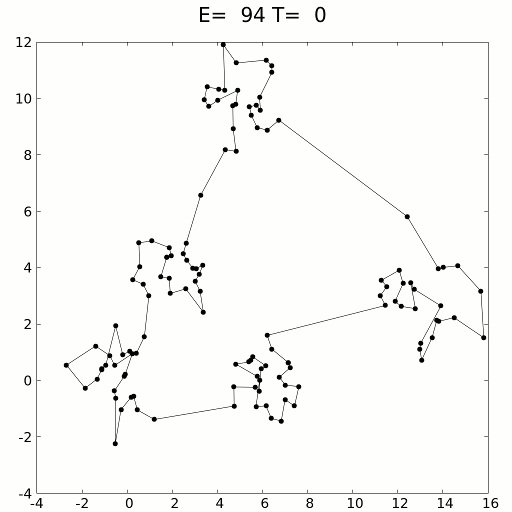
#Реализация
На практике применим алгоритм к другой задаче:
Дана шахматная доска $n \times n$ и $n$ ферзей. Нужно расставить их так, чтобы они не били друг друга.
Будем кодировать состояние так же перестановкой чисел от $0$ до $(n-1)$: ферзь номер $i$ будет стоять на пересечении $i$-той строки и $p_i$-того столбца.
Такое представление кодирует не все возможные расстановки, но это даже хорошо: точно не учтутся те расстановки, где ферзи бьют друг друга по вертикали или горизонтали.
Выберем функцию $f(p)$, равную числу успешно расставленных ферзей.
Примерно эквивалентный код на C++:
const int n = 100; // размер доски
const int k = 1000; // количество итераций алгоритма
int f(vector<int> &p) {
int s = 0;
for (int i = 0; i < n; i++) {
int d = 1;
for (int j = 0; j < i; j++)
if (abs(i - j) == abs(p[i] - p[j]))
d = 0;
s += d;
}
return s;
}
// генерирует действительное число от 0 до 1
double rnd() { return double(rand()) / RAND_MAX; }
int main() {
// генерируем начальную перестановку
vector<int> v(n);
iota(v.begin(), v.end(), 0);
shuffle(v.begin(), v.end());
int ans = f(v); // текущий лучший ответ
double t = 1;
for (int i = 0; i < k && ans < n; i++) {
t *= 0.99;
vector<int> u = v;
swap(u[rand() % n], u[rand() % n]);
int val = f(u);
if (val > ans || rnd() < exp((val - ans) / t)) {
v = u;
ans = val;
}
}
for (int x : v)
cout << x + 1 << " ";
return 0;
}
Здесь подсчёт количества свободных диагоналей работает за $O(n^2)$. Его можно соптимизировать до $O(n)$ и делать в $O(n)$ итераций больше: можно создать булев массив, в котором для каждой диагонали хранить, была ли она занята. С этой оптимизацией уже должна быть сдаваема эта задача на информатиксе.
Упражнение. Соптимизируйте пересчёт до $O(1)$.
Примечание. На самом деле, задача о ферзях решается конструктивно.