Метод копирования пути

В широком смысле, структура данных — это набор связанных ссылками узлов, в которых хранятся данные.

Обычный массив тоже попадает под это определение: в нём узел один, в котором хранятся $n$ ячеек.

Рассмотрим немного более узкий класс структур, в котором каждый узел хранит $O(1)$ полей и ссылок. Например, дерево отрезков и декартово дерево, которые мы рассмотрим далее, удовлетворяют этому свойству.

Для таких структур существует простой и общий способ сделать их полностью персистентными — метод копирования путей.

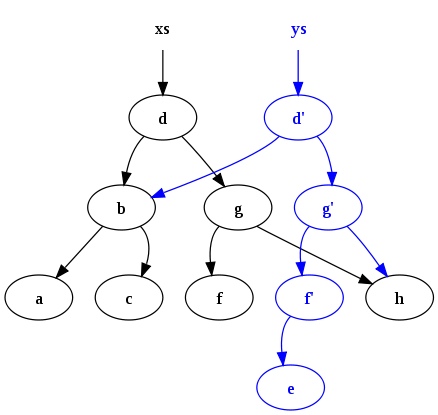
Рассмотрим в качестве примера сбалансированные деревья. Пусть необходимо сделать какое-то обновление — например, добавить очередной элемент — но при этом нужно не потерять никакую информацию про старое дерево.

Возьмем вершину, к которой нужно добавить нового ребенка. Вместо того чтобы добавлять нового ребенка напрямую в её, скопируем весь путь от корня до этой вершины вместе со всеми данными и указателями, а затем добавим ребенка к соответствующей вершине в скопированном пути. Все остальные вершины, из которых измененный узел не достижим, мы не трогаем.

В результате такой операции из нового корня достижимы все вершины обновленного дерева, а из старого корня и всех ранее существовавших вершин достижимы ровно те же неизмененные вершины, что и раньше — мы ведь ничего не удаляли и не меняли, а всего лишь создали порядка логарифма новых вершин.

Если после каждой операции складывать корни дерева в какой-нибудь отдельный массив, то мы получаем доступ к произвольным предыдущим версиям, от которых можно свободно «форкаться».

#Асимптотика

В большинстве операций нам и так нужно делать логарифм работы, так что асимптотика по времени не изменится, хотя расход памяти увеличивается до $O(n \log n)$.

На практике же персистентные структуры могут быть значительно (в 2-5 раз) медленнее, потому что данные перестают переиспользоваться, из-за чего почти исчезает выгода от кэшей процессора.

Также в персистентных структурах в худшем случае не работает амортизация: если есть какая-то тяжелая операция (например «сжатие бамбука»), то можно много раз откатываться до её и повторять. Поэтому структуры вроде системы непересекающихся множеств и splay-дерева будут иметь худшую асимптотику.

#Персистентный стек

Реализацию и применение персистентных деревьев рассмотрим в следующих статьях, а пока в учебных целях применим метод к стеку.

Помимо массива с указателем на последний элементы, стек также тоже можно реализовать на ссылках. В этом случае «корень» стека — это его верхний элемент.

struct Node {
    int val;
    Node *prev;
};

Node *head;

void add(int x) {
    head = new Node(x, head);
}

int top() {
    return head.val;
}

void pop() {
    Node *old = head;
    head = head->prev; // если на память пофиг, можно оставить только эту строчку
    delete old;
}

Теперь, чтобы сделать стек персистентным, дополнительные поля нам не нужны, но понадобится добавить глобальный массив версий и дополнительный параметр во все методы:

vector<Node*> versions;

void add(int x, int v);
int top(int v);
void pop(int v);

Чтобы сделать ссылочную структуру персистентной, нужно изменить только те операции, которые как-то меняют её состояние — в нашем случае это add и pop.

Для add нужно воспользоваться такой же процедурой, но создать новую вершину вместо перезаписи head:

void add(int x, int v) {
    versions.push_back(new Node(x, versions[v]));
}

Для pop можно поступить так же, но можно и схитрить, просто добавив в конец списка версий ссылку на уже существующий узел:

void pop(int v) {
    versions.push_back(versions[v]->prev);
}

Обе операции работают за $O(1)$ времени и дополнительной памяти.

Используя персистентный стек, можно легко реализовать персистентную очередь (через два персистентных стека), однако за счёт амортизации она будет работать за $O(n)$ на операцию в худшем случае. Также есть сложные способы реализовать очередь на пяти или шести стеках с чистым $O(1)$ времени на операцию.