Назовем подграф графа безопасным, если он является подграфом какого-то минимального остова.
Назовем ребро безопасным, если при добавлении его в подграф получившийся подграф тоже является безопасным, то есть подграфом какого-то минимального остова.
Разрезом связного графа будем называть подмножество рёбер и вершин, образующих подграф, в котором есть ровно две компоненты связности. Ребро пересекает данный разрез, если при его добавлении граф снова становится связным.
Все алгоритмы для поиска минимального остова опираются на следующее утверждение:
Лемма о безопасном ребре. Рассмотрим произвольный разрез какого-либо подграфа минимального остова. Тогда ребро минимального веса, пересекающее этот разрез, является безопасным.
Доказательство: Рассмотрим какой-то минимальный остов, в котором этого ребра нет. Если его добавить, то образуется цикл, из которого можно удалить ребро не меньшего веса, получив ответ точно не хуже. Противоречие.
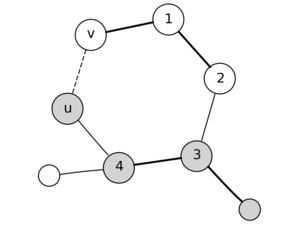
Получается, что для построения минимального остова мы можем действовать жадно: на каждом шаге добавлять ребро минимального веса, которое увеличивает уже построенную часть остова. Есть несколько способов это сделать, о которых мы поговорим дальше.
#Следствия
- Если веса всех рёбер различны, то остов будет уникален.
- Минимальный остов является также и остовом с минимальным произведением весов рёбер (замените веса всех рёбер на их логарифмы).
- Минимальный остов является также и остовом с минимальным весом самого тяжелого ребра.
- Остовные деревья — частный случай матроидов.