Метод сканирующей прямой (англ. scanline) заключается в сортировке точек на координатной прямой либо каких-то абстрактных «событий» по какому-то признаку и последующему проходу по ним.
Он часто используется для решения задач на структуры данных, когда все запросы известны заранее, а также в геометрии для нахождения объединений фигур.
#Точка, покрытая наибольшим количеством отрезков
Задача. Дан набор из $n$ отрезков на прямой, заданных координатами начал и концов $[l_i, r_i]$. Требуется найти любую точку на прямой, покрытую наибольшим количеством отрезков.
Рассмотрим функцию $f(x)$, равную числу отрезков, покрывающих точку $x$. Понятно, что каждую точку этой функции мы проверить не можем.
Назовем интересными те точки, в которых происходит смена количества отрезков, которыми она покрыта. Так как смена ответа может происходить только в интересной точке, то максимум достигается также в какой-то из интересных точек. Отсюда сразу следует решение за $O(n^2)$: просто перебрать все интересные точки (это будут концы заданных отрезков) и проверить для каждой по отдельности ответ.
Это решение можно улучшить. Отсортируем интересные точки по возрастанию координаты и пройдем по ним слева направо, поддерживая количество отрезков cnt, которые покрывают данную точку. Если в данной точке начинается отрезок, то надо увеличить cnt на единицу, а если заканчивается, то уменьшить. После этого пробуем обновить ответ на задачу текущим значением cnt.
Как такое писать: нужно представить интересные точки в виде структур с полями «координата» и «тип» (начало / конец) и отсортировать со своим компаратором. Удобно начало отрезка обозначать +1, а конец -1, чтобы просто прибавлять к cnt это значение и не разбивать на случаи.
Единственный нюанс — если координаты двух точек совпали, чтобы получить правильный ответ, сначала надо рассмотреть все начала отрезков, а только потом концы (чтобы при обновлении ответа в этой координате учлись и правые, и левые граничные отрезки).
struct event {
int x, type;
};
int scanline(vector<pair<int, int>> segments) {
vector<event> events;
for (auto [l, r] : segments) {
events.push_back({l, 1});
events.push_back({r, -1});
}
sort(events.begin(), events.end(), [](event a, event b) {
return (a.x < b.x || (a.x == b.x && a.type > b.type));
});
int cnt = 0, res = 0;
for (event e : events) {
cnt += e.type;
res = max(res, cnt);
}
return res;
}
Такое решение работает за $O(n \log n)$ на сортировку. Если координаты небольшие, то от логарифма можно избавиться, если создать vector событий для каждой различной координаты и просто итерироваться по всем целочисленным координатам и событиям в них. Также всегда хорошей идеей будет сжать координаты.
Рассмотрим теперь несколько смежных задач.
#Длина объединения отрезков
Задача. Дан набор из $n$ отрезков на прямой, заданных координатами начал и концов $[l_i, r_i]$. Требуется найти суммарную длину их объединения.
Как и в прошлой задаче, отсортируем все интересные точки и при проходе будем поддерживать число отрезков, покрывающих текущую точку. Если оно больше 0, то отрезок, который мы прошли с прошлой рассмотренной точки, принадлежит объединению, и его длину нужно прибавить к ответу:
int cnt = 0, res = 0, prev = -inf;
for (event e : events) {
if (prev != -inf && cnt > 0)
res += e.x - prev; // весь отрезок [prev, e.x] покрыт cnt отрезками
cnt += e.type;
prev = e.x;
}
Время работы $O(n \log n)$.
#Скольким отрезкам принадлежит точка
Пусть теперь надо для $q$ точек (не обязательно являющихся концами отрезков) ответить на вопрос: скольким отрезкам принадлежит данная точка?
Воспользуемся следующим приемом: сразу считаем все запросы и сохраним их, чтобы потом ответить на все сразу. Добавим точки запросов как события с новым типом 0, который будет означать, что в этой точке надо ответить на запрос, и отдельным полем для номера запроса.
Теперь аналогично отсортируем точки интереса и пройдем по ним слева направо, поддерживая cnt и отвечая на запросы, когда их встретим.
struct event {
int x, type, idx;
};
void scanline(vector<pair<int, int>> segments, vector<int> queries) {
int q = (int) queries.size();
vector<int> ans(q)
vector<event> events;
for (auto [l, r] : segments) {
events.push_back({l, 1});
events.push_back({r, -1});
}
for (int i = 0; i < q; i++)
events.push_back({queries[i], 0, i});
// при равенстве координат сначала идут добавления, потом запросы, потом удаления
sort(events.begin(), events.end(), [](event a, event b) {
return (a.x < b.x || (a.x == b.x && a.type > b.type));
});
int cnt = 0;
for (event e : events) {
cnt += e.type;
if (e.type == 0)
ans[e.idx] = cnt;
}
}
Асимптотика $O((n+q)\log(n+q))$.
#Количество пересекающихся отрезков
Задача. Дан набор из $n$ отрезков на прямой, заданных координатами начал и концов $[l_i, r_i]$. Требуется для каждого отрезка сказать, с каким количеством отрезков он пересекается (в частности, он может иметь одну общую точку или быть вложенным).
Вместо того, чтобы для каждого отрезка считать количество отрезков, с которыми он пересекается, посчитаем количество отрезков, с которыми он не пересекается, и вычтем это число из $(n-1)$.
Отрезок $[l_1, r_1]$ не пересекается с другим отрезком $[l_2, r_2]$ только если $r_2 < l_1$ или $r_1 < l_2$. Посчитаем количество отрезков для каждого из этих случаев. Без ограничения общности, рассмотрим первый случай, то есть найдем для каждого отрезка количество отрезков, лежащих строго слева. Для этого нужно ввести два типа событий:
- Какой-то отрезок закончился в координате $r_i$.
- Какой-то отрезок с таким-то индексом начался в координате $l_j$.
Теперь нам достаточно пройтись по этим событиям слева направо, поддерживая количество встреченных событий первого типа и вычитая его из ячейки ответа для событий второго типа.
Аналогично пройдемся справа налево, находя отрезки, лежащие строго справа. Итоговое время работы будет $O(n \log n)$ на сортировку.
#Сумма на прямоугольнике
Перейдем к двумерному сканлайну.
Задача. Даны $n$ точек на плоскости. Требуется ответить на $m$ запросов количества точек на прямоугольнике.
Во-первых, сожмем все координаты (и точек, и запросов): будем считать, что они все порядка $O(n + m)$.
Теперь разобьём каждый запрос на два запроса суммы на префиксах: сумма на прямоугольнике $[x_1, x_2] \times [y_1, y_2]$ равна сумме на прямоугольнике $[0, x_2] \times [y_1, y_2]$ минус сумме на прямоугольнике $[0, x_1] \times [y_1, y_2]$.
Создадим дерево отрезков для суммы и массив ans для ответов на запросы. Теперь будем проходиться в порядке увеличения по всем интересным $x$ — координатам точек и правых границ префиксных запросов — и обрабатывать события трёх типов:
- Если мы встретили точку, то добавляем единицу к ячейке $y$ в дереве отрезков.
- Если мы встретили «левый» запрос префиксной суммы, то посчитаем через дерево отрезков сумму на отрезке $[y_1, y_2]$ и вычтем его из ячейки ответа.
- Если мы встретили «правый» запрос, то аналогично прибавим сумму на $[y_1, y_2]$ к ячейке ответа.
Таким образом, мы решим задачу в оффлайн за $O(n \log n)$: сжатие координат / сортировка плюс $O(n)$ запросов к дереву отрезков (или любой другой структуре для динамической суммы).
Сумма на прямоугольнике как вспомогательная подзадача также часто используется в задачах на инверсии в перестановках и запросы на поддеревьях.
#Площадь объединения прямоугольников
Задача. Дано $n$ прямоугольников, требуется найти площадь их объединения.
Вдохновляясь предыдущим подходом, можно создать два типа событий:
- прямоугольник с $y$-координатами от $y_1$ до $y_2$ начинается в точке $x_1$;
- прямоугольник с $y$-координатами от $y_1$ до $y_2$ заканчивается в точке $x_2$;
и затем как-то пройтись по этим событиям в порядке увеличения $x$ и посчитать общую площадь подобно тому, как мы делали с одномерными отрезками.
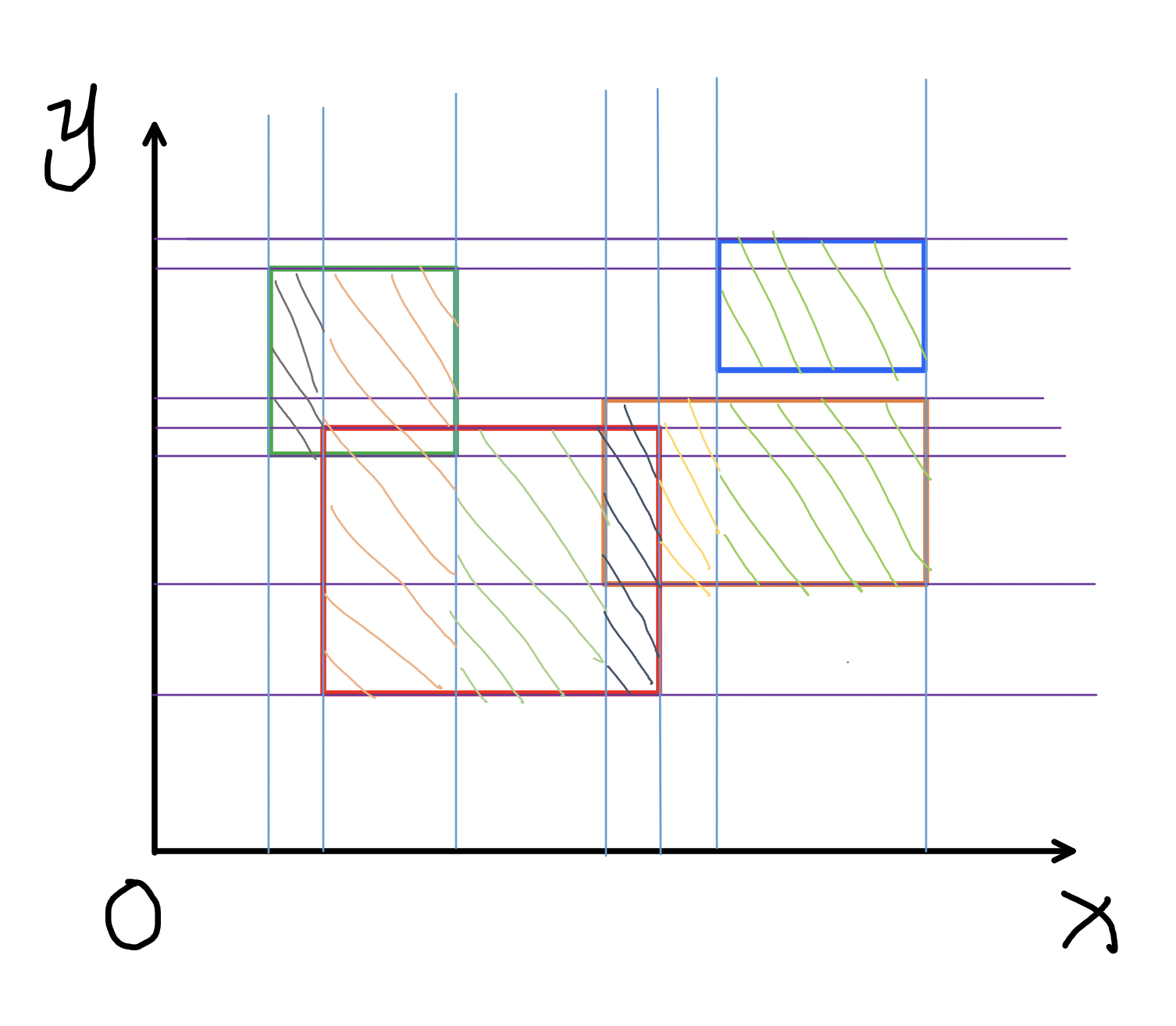
Если обобщать подход напрямую, то нам нужно завести массив размера $Y$ (максимальной $y$-координаты) и для каждой $y$-параллели поддерживать число прямоугольников, которые её покрывают, и каждый раз, когда $x$-координата события меняется, добавлять к ответу разницу $x$-координат старого и нового события, помноженную на число ненулевых элементов в массиве (точек на вертикальной сканирующей прямой, которые покрываются хотя бы одним прямоугольником).
Но это в худшем случае работает за $O(nY)$, что достаточно долго. Чтобы получить более приятную асимптотику, заменим массив деревом отрезков, в узлах которого будет храниться минимум и число элементов с таким минимумом (изначально минимум 0 и таких элементов на всём массиве $Y$).
Чтобы обновить ответ, нужно помножить разницу $x$-координат соседних событий на число ненулевых элементов, которое можно найти, вычтя из $Y$ количество минимумов-нулей на всём дереве. Одномерная задача пересчета этой информации при прибавлениях на отрезке остается упражнением читателю.
Такой алгоритм работает за $O(n \log n)$, если аккуратно сжать координаты, и за $O(n \log Y)$, если этого не делать. Этот метод также обобщается на задачу нахождения площадей и других геометрических фигур.