Быстрое преобразование Фурье

Быстрое преобразование Фурье — один из самых важных алгоритмов XX века, если не самый важный.

Оно применяется, как можно догадаться, для вычисления преобразований Фурье, которые в свою очередь используются для обработки звука, электромагнитных волн, задач оптики, сжатия данных, физического моделирования и прочих сложных математических и физических задач.

В этой статье же мы подойдем немного с другой стороны и рассмотрим алгоритм быстрого преобразования Фурье в контексте задачи умножения чисел и многочленов, часто встречающейся в олимпиадах.

#Умножение через интерполяцию

Многочлен степени $(n - 1)$ можно однозначно задать не только своими коэффициентами, но и значениями в $n$ различных точках.

При прямом перемножении многочленов, заданных своими коэффициентами, нужно потратить $O(n^2)$ операций. Но если многочлены заданы своими значениями в $2n$ точках, то их можно перемножить за $O(n)$: значение многочлена-произведения $A(x) \cdot B(x)$ в точке $x_i$ просто становится равным $A(x_i) \cdot B(x_i)$.

Основная идея алгоритма заключается в том, что если мы посчитаем значения в каких-то различных $(n + m)$ точках для обоих многочленов $A$ и $B$, то, попарно перемножив их, мы за $O(n + m)$ операций можем получить значения в тех же точках для многочлена $A(x) \cdot B(x)$, и с их помощью интерполяцией получить коэффициенты многочлена-произведения и решить задачу.

vector<int> poly_multiply(vector<int> a, vector<int> b) {
    vector<int> A = evaluate(a);
    vector<int> B = evaluate(b);
    for (int i = 0; i < A.size(); i++)
        A[i] *= B[i];
    return interpolate(A);
}

Если притвориться, что evaluate и interpolate работают за линейное время, то такое умножение тоже будет работать за линейное время. Но, к сожалению, непосредственное вычисление значений требует $O(n^2)$ операций, а интерполяция — как методом Гаусса, так и через символьное вычисление многочлена Лагранжа — и того больше, $O(n^3)$.

Но что, если бы мы могли вычислять значения в точках и делать интерполяцию быстрее? Выясняется, что это можно сделать, если рассматривать не произвольные точки, а только специальные — а именно, комплексные корни из единицы.

#Корни из единицы

Факт. Для любого натурального $n$ есть ровно $n$ «корней из единицы», то есть чисел $w_k$, для которых

$$ w_k^n = 1 $$ А именно, это будут числа вида $$ w_k = e^{i \tau \frac{k}{n}} $$

где $\tau$ обозначает $2 \pi$, «целый круг». Это довольно новая нотация.

На комплексной плоскости эти числа располагаются на единичном круге на равном расстоянии друг от друга:

Все 9 комплексных корней степени 9 из единицы

Первый корень $w_1$ (точнее второй — единицу считаем нулевым корнем) называют образующим корнем степени $n$ из единицы. Возведение его в нулевую, первую, вторую и так далее степени порождает последовательность нужных корней единицы, при этом на $n$-ном элементе последовательность зацикливается:

$$ w_n = e^{i \tau \frac{n}{n}} = e^{i \tau} = e^{i \cdot 0} = w_0 = 1 $$

Будем обозначать $w_1$ как просто $w$.

#Дискретное преобразование Фурье

Дискретным преобразованием Фурье собственно и называется вычисление значений многочлена в комплексных корнях из единицы:

$$ y_j = \sum_{k=0}^{n-1} x_k e^{i\tau \frac{kj}{n}} = \sum_{k=0}^{n-1} x_k w_1^{kj} $$

Обратным дискретным преобразованием Фурье называется, как можно догадаться, обратная операция — интерполяция коэффициентов $x_i$ по значениям $y_i$.

Утверждение. Обратное ДПФ можно вычислить по формуле

$$ x_j = \frac{1}{n} \sum_{k=0}^{n-1} y_k e^{-i\tau \frac{kj}{n}} = \frac{1}{n} \sum_{k=0}^{n-1} y_k w_{n-1}^{kj} $$ Доказательство. При вычислении ПФ мы фактически применяем матрицу к вектору: $$ \begin{pmatrix} w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^1 & w^2 & w^3 & \dots & w^{-1} \\ w^0 & w^2 & w^4 & w^6 & \dots & w^{-2} \\ w^0 & w^3 & w^6 & w^9 & \dots & w^{-3} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^{-1} & w^{-2} & w^{-3} & \dots & w^1 \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1} \end{pmatrix} = \begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{pmatrix} $$

То есть преобразование Фурье — это просто линейная операция над вектором: $W a = y$. Значит, обратное преобразование можно записать так: $a = W^{-1}y$.

Как будет выглядеть эта $W^{-1}$? Автор не будет пытаться изображать логичный способ рассуждений о её получении и сразу её приведёт:

$$ W^{-1} = \dfrac 1 n \begin{pmatrix} w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^{-1} & w^{-2} & w^{-3} & \dots & w^{1} \\ w^0 & w^{-2} & w^{-4} & w^{-6} & \dots & w^{2} \\ w^0 & w^{-3} & w^{-6} & w^{-9} & \dots & w^{3} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^{1} & w^{2} & w^{3} & \dots & w^{-1} \end{pmatrix} $$

Проверим, что при перемножении $W$ и $W^{-1}$ действительно получается единичная матрица:

Значение $i$-того диагонального элемента будет равно $\frac{1}{n} \sum_k w^{ki} w^{-ki} = \frac{1}{n} n = 1$.
Значение любого недиагонального ($i \neq j$) элемента $(i, j)$ будет равно

$$ \frac{1}{n} \sum_k w^{ik} w^{-jk} = \frac{1}{n} \sum_k w^k w^{i-j} = \frac{w^{i-j}}{n} \sum_k w^k = 0 $$

Последний переход верен, потому что все комплексные корни суммируются в ноль, то есть $\sum w^k = 0$.

Внимательный читатель заметит симметричность форм $W$ и $W^{-1}$, а также формул для прямого и обратного преобразования. Эта симметрия нам сильно упростит жизнь: для обратного преобразования Фурье можно использовать тот же алгоритм, только вместо $w^k$ использовать $w^{-k}$, а в конце результат поделить на $n$.

#Алгоритм

Напомним, что мы изначально хотели перемножать многочлены следующим алгоритмом:

Посчитаем значения в $(n+m)$ каких-нибудь точках обоих многочленов.
Перемножим эти значения попарно за $O(n + m)$.
Интерполяцией получим многочлен-произведение.

В общем случае быстро посчитать интерполяцию и даже просто посчитать значения в точках нельзя, но для корней единицы — можно. Если научиться быстро считать значения в корнях и интерполировать (прямое и обратное преобразование Фурье), но мы сможем решить исходную задачу.

Соответствующий алгоритм и называется быстрым преобразованием Фурье (англ. fast Fourier transform). Он использует парадигму «разделяй-и-властвуй» и работает за $O(n \log n)$.

#Схема Кули-Тьюки

Обычно, алгоритмы «разделяй-и-властвуй» делят задачу на две половины: на первые $\frac{n}{2}$ элементов и вторые $\frac{n}{2}$ элементов. Здесь же мы поступим по-другому: поделим все элементы на чётные и нечётные.

Представим многочлен в виде $P(x)=A(x^2)+xB(x^2)$, где $A(x)$ состоит из коэффициентов при чётных степенях $x$, а $B(x)$ — из коэффициентов при нечётных.

Пусть $n = 2k$. Тогда заметим, что для любого целого числа $t$

$$ w^{2t} = w^{2t \bmod n} = w^{2t \bmod 2k} = w^{2(t \bmod k)} $$ Зная это, исходную формулу для значения многочлена в точке $w^t$ можно записать так: $$ P(w^t) = A(w^{2t}) + w^t B(w^{2t}) = A\left(w^{2(t\bmod k)}\right)+w^tB\left(w^{2(t\bmod k)}\right) $$

Ключевое замечание: различных корней вида $w^{2t}$, значения в которых нам потребуются для пересчета, будет в два раза меньше, а также в обоих многочленах будет в два раза меньших коэффициентов — значит, мы только что успешно разбили нашу задачу на две, каждая из которых в два раза меньше.

Сам алгоритм заключается в следующем: рекурсивно посчитаем БПФ для многочленов $A$ и $B$ и объединим ответы с помощью формулы выше. При этом в рекурсии нам нужно считать значения на корнях степени не $n$, а $k = \frac{n}{2}$, то есть на всех «чётных» корнях степени $n$ (вида $w^{2t}$). Заметим, что если $w$ это образующий корень степени $n = 2k$ из единицы, то $w^2$ будет образующим корнем степени $k$, то есть в рекурсию мы можем просто передать другое значение образующего корня.

Таким образом, мы свели преобразование размера $n$ к двум преобразованиям размера $\dfrac n 2$, и, следовательно, общее время вычисления БПФ составит

$$ T(n)=2T\left(\dfrac n 2\right)+O(n)=O(n\log n) $$

Отметим также, что предположение о делимости $n$ на $2$ имело существенную роль. Значит, $n$ должно быть чётным на каждом уровне, кроме последнего, из чего следует, что $n$ должно быть степенью двойки.

#Реализация

Приведём код, вычисляющий БПФ по схеме Кули-Тьюки:

typedef complex<double> ftype;
const double pi = acos(-1);

// принимает массив и n-ный корень из единицы, и заменяет его на значения в корнях
void fft(vector<ftype> &p, ftype wn) {
    int n = (int) p.size();
    if (n == 1)
        return;
    // разделяем массив на четный и нечетный
    vector<ftype> a(n / 2), b(n / 2);
    for (int i = 0; i < n / 2; i++) {
        a[i] = p[2 * i];
        b[i] = p[2 * i + 1];
    }
    // рекурсивно считаем БПФ
    fft(a, wn * wn);
    fft(b, wn * wn);
    // объединяем результат по формуле
    ftype w = 1;
    for (int i = 0; i < n / 2; i++) {
        // можно не использовать модуль, а сразу раскрыть его для двух половин
        p[i] = a[i] + w * b[i];
        p[i + n / 2] = a[i] - w * b[i]; // w^(i+n/2) = -w^i
        w *= wn;
    }
}

При изначальном запуске следует дополнить массив до степени двойки:

vector<ftype> evaluate(vector<int> p) {
    while (__builtin_popcount(p.size()) != 1)
        p.push_back(0);
    return fft(p, polar(1., 2 * pi / p.size()));
}

Как обсуждалось ранее, обратное преобразование Фурье удобно выразить через прямое:

vector<int> interpolate(vector<ftype> p) {
    int n = p.size();
    auto inv = fft(p, polar(1., -2 * pi / n));
    vector<int> res(n);
    for(int i = 0; i < n; i++)
        // мы хотим получать целые числа, для этого результаты нужно округлить
        res[i] = round(real(inv[i]) / n);
    return res;
}

Теперь мы умеем перемножать два многочлена за $O(n \log n)$:

vector<int> poly_multiply(vector<int> a, vector<int> b) {
    vector<ftype> A = evaluate(a);
    vector<ftype> B = evaluate(b);
    for (int i = 0; i < A.size(); i++)
        A[i] *= B[i];
    return interpolate(A);
}

Приведённый выше код, являясь корректным и имея асимптотику $O(n \log n)$, имеет весьма большую константу — в основном из-за рекурсии и дополнительных аллокаций.

#Оптимизированная версия

Попробуем избавиться от аллокаций вообще. Сейчас они происходят, потому что мы каждый раз разбиваем массив на два. Что произойдет, если вместо того, чтобы создавать новые массивы, просто сдвинуть все четные элементы в левую половину, а нечетные — в правую, и запуститься рекурсивно от половин?

Наблюдение. Элемент с индексом k на последнем уровне рекурсии будет записан в ячейку revbits(k), где функция revbits(x) «разворачивает» биты числа x.

Действительно, первой итерации все четные элементы (с нижним битом, равным нулю) будут записаны в первую половину (в позицию с верхним битом, равным нулю), а для нечетных наоборот. Дальше, все элементы со вторым самым младшим битом равным нулю будут внутри своих половин записаны в меньшую половину (со вторым самым старшим битом, равным нулю), и так далее.

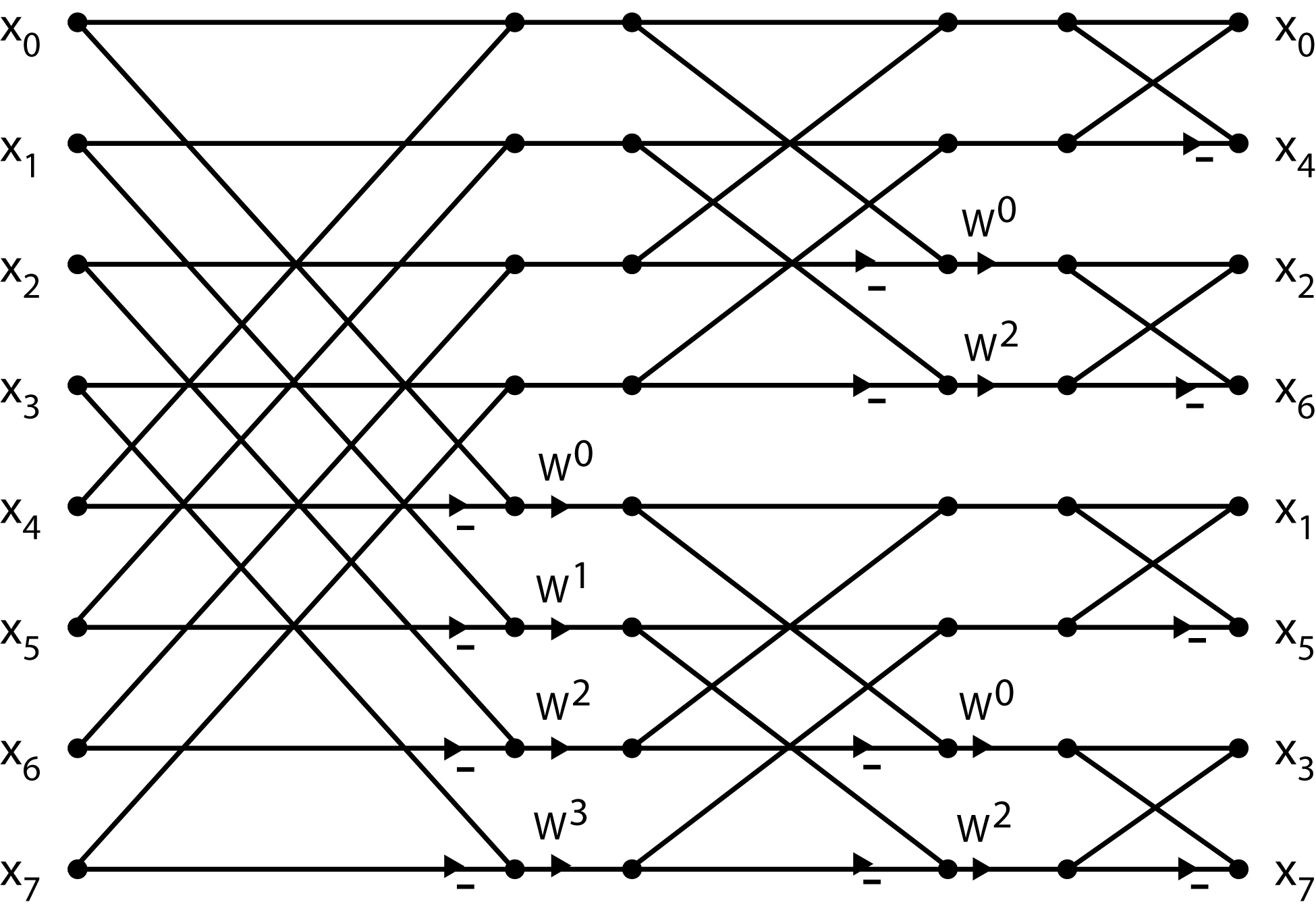
Если мы знаем, где окажется каждый элемент, то давайте тогда даже не будем делать какие-либо перестановки внутри рекурсии, а просто выполним их один раз в самом начале, а в рекурсивной функции будем просто запускаться от половин.

void solve(ftype *a, int n, ftype wn) {
    if (n > 1) {
        int k = (n >> 1);
        solve(a, k, wn * wn);
        solve(a + k, k, wn * wn);
        ftype w = 1;
        for (int i = 0; i < k; i++) {
            // тут нужно быть чуть аккуратней с перезаписыванием,
            // потому что мы читаем и пишем из одного и того же массива
            ftype t = w * a[i + k];
            a[i + k] = a[i] - t; 
            a[i] = a[i] + t;
            w *= wn;
        }
    }
}

void fft(ftype *a, int n, int inverse) {
    const int logn = __lg(n);

    for (int i = 0; i < n; i++) {
        // переворачиваем биты числа i
        int k = 0;
        for (int l = 0; l < logn; l++)
            k |= ((i >> l & 1) << (logn - l - 1));
        // делаем только один swap -- из того элемента, который идет раньше
        if (i < k)
            swap(a[i], a[k]);
    }

    ftype wn = polar(1., inverse * 2 * pi / n); // inverse = {-1, +1}
    solve(a, n, wn);
}

У алгоритма довольно неплохая численная стабильность, однако в олимпиадных задачах часто требуется считать какой-нибудь большой целочисленный ответ, либо посчитать его по модулю. Однако от этой проблемы можно избавиться.

#Number-theoretic transform

Нам от комплексных чисел на самом деле нужно было только одно свойство: что у единицы есть $n$ «корней». На самом деле, помимо комплексных чисел, есть и другие алгебраические объекты, обладающие таким свойством — например, элементы кольца вычетов по модулю.

Найдем пару $m$ и $g$ (играющее роль $w_n^1$), такую что $g$ является образующим элементом, то есть $g^n \equiv 1 \pmod m$ и для всех остальных $k < n$ все степени $g^k$ различны по модулю $m$. В качестве $m$ на практике часто специально берут «удобные» модули, например

$$ m = 998244353 = 7 \cdot 17 \cdot 2^{23} + 1 $$

Это число простое, и при этом является ровно на единицу больше числа, делящегося на большую степень двойки. При $n=2^{23}$ подходящим $g$ является число $31$. Заметим, что, как и для комплексных чисел, если для некоторого $n=2^k$ первообразный корень $g$, то для $n=2^{k-1}$ первообразным корнем будет $(g^2 \bmod m)$. Таким образом, для $m=998244353$ и $n=2^k$ первообразный корень будет равен $g=31^{2^{23-k}} \bmod m$.

Реализация при этом практически не отличается: нужно просто использовать модулярную арифметику во всех операциях и страшные предподсчитанные константы для $w$ и $w^{-1}$.

Также с недавнего времени некоторые проблемсеттеры начали использовать именно этот модуль вместо стандартного $10^9+7$, чтобы намекнуть (или сбить с толку), что задача на FFT.