Компонентой связности неориентированного графа называется подмножество вершин, достижимых из какой-то заданной вершины. Как следствие неориентированности, все вершины компоненты связности достижимы друг из друга.
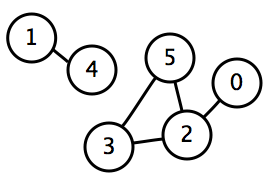
Дан неориентированный граф $G$ с $n$ вершинами и $m$ рёбрами. Требуется найти в нём все компоненты связности, то есть разбить вершины графа на несколько групп так, что внутри одной группы можно дойти от одной вершины до любой другой, а между разными группами путей не существует.
Для решения задачи модифицируем обход в глубину так, чтобы запустившись от вершины какой-то компоненты, от пометил все вершины этой компоненты — то есть все достижимые вершины — заданным номером этой компоненты. Для этого можно массив used заменить массивом номеров компонент для каждой вершины, изначально заполненный нулями:
const int maxn = 1e5;
int component[maxn]; // тут будут номера компонент
void dfs(int v, int num) {
component[v] = num;
for (int u : g[v])
if (!component[u]) // если номер не присвоен, то мы там ещё не были
dfs(u, num);
}
Теперь проведем серию обходов: сначала запустим обход из первой вершины, и все вершины, которые он при этом обошёл, образуют первую компоненту связности. Затем найдём первую из оставшихся вершин, которые ещё не были посещены, и запустим обход из неё, найдя тем самым вторую компоненту связности. И так далее, пока все вершины не станут помеченными.
Записывается это очень компактно:
int num = 0;
for (int v = 0; v < n; v++)
if (!component[v])
dfs(v, ++num);
После этого переменная num будет хранить число компонент связности, а массив component — номер компоненты для каждой вершины, который, например, можно использовать, чтобы быстро проверять, существует ли путь между заданной парой вершин.
Итоговая асимптотика составит $O(n + m)$, потому что такой алгоритм не будет запускаться от одной и той же вершины дважды, и каждое ребро будет просмотрено ровно два раза (с одного конца и с другого).