Алгоритм Грэхэма

Алгоритм Грэхэма — это оптимизация алгоритма Джарвиса, основанная на следующем наблюдении: если отсортировать все точки по полярному углу относительно точки $p_0$, то выпуклая оболочка будет какой-то подпоследовательностью такого отсортированного массива точек.

Алгоритм последовательно строит выпуклые оболочки для каждого префикса этого отсортированного массива. Можно заметить, что при добавлении $i$-й точки в оболочку нужно лишь удалить сколько-то последних добавленных точек, которые не будут входить в новую оболочку, а именно тех, которые «покрываются» новой точкой и своей предыдущей.

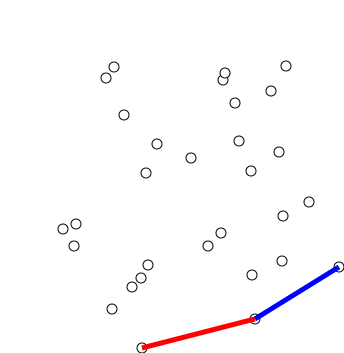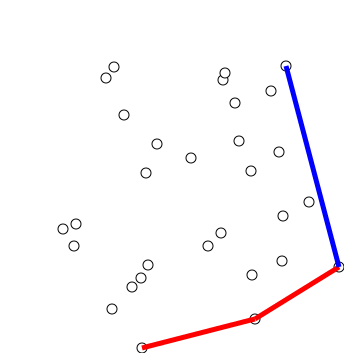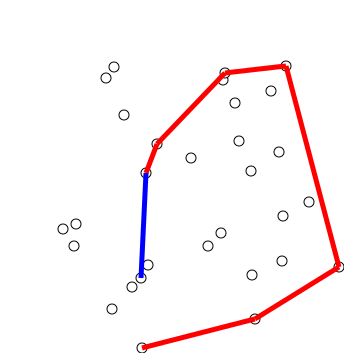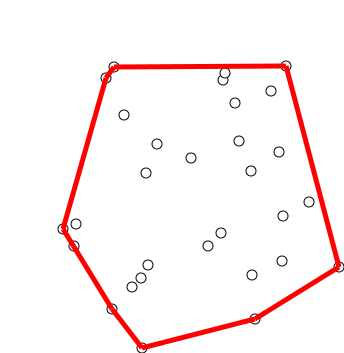
Чтобы проводить это удаление эффективно, мы можем хранить выпуклую оболочку в стеке и в цикле while смотреть на три последние точки и проверять, образуют ли они правый поворот. Если это так, то среднюю следует удалить — мы нашли треугольник $(p_0, p_i, p_{i-2})$, который содержит $p_{i-1}$, а значит её можно удалить.

Каждая точка будет добавлена один раз удалена не более одного раза, что занимает константное количество операций. Соответственно, время работы будет упираться во время работы сортировки, то есть $O(n \log n)$.

vector<r> graham(vector<r> points) {
    // находим p0, как и раньше
    r p0 = points[0];
    for (r p : points)
        if (p.x < p0.x || (p.x == p0.x && p.y < p0.y))
            p0 = p;

    // сортируем точки по полярному углу
    sort(points.begin(), points.end(), [&](r a, r b){
        return (a - p0) ^ (b - p0) > 0;
    });

    vector<r> hull;
    for (r p : points) {
        // удаляем последнюю точку со стека пока она образует невыпуклость
        while (hull.size() >= 2) {
            r new_vector = p - hull.back();
            r last_vector = hull.back() - hull[hull.size() - 2];
            // если два последних вектора заворачивают влево, удаляем последнюю точку
            if (new_vector ^ last_vector > 0)
                hull.pop_back();
            else
                break;
        }
        hull.push_back(p);
    }
    return hull;
}

Интерактивная визуализация, где на заданном наборе точек прогоняются все шаги алгоритма.