Система непересекающихся множеств (англ. disjoint set union) — структура данных, позволяющая объединять непересекающиеся множества и отвечать на разные запросы про них, например «находятся ли элементы и в одном множестве» и «чему равен размер данного множества».
Более формально, изначально имеется элементов, каждый из которых находится в отдельном (своём собственном) множестве. Структура поддерживает две базовые операции:
- Объединить два каких-либо множества.
- Запросить, в каком множестве сейчас находится указанный элемент.
Обе операции выполняются в среднем почти за (но не совсем).
СНМ часто используется в графовых алгоритмах для хранения информации о связности компонент — например, в алгоритме Краскала.
#Устройство структуры
Множества элементов мы будем хранить в виде деревьев: одно дерево соответствует одному множеству. Корень дерева — это представитель (лидер) множества. Для корней деревьев будем считать, что их предки — они сами.
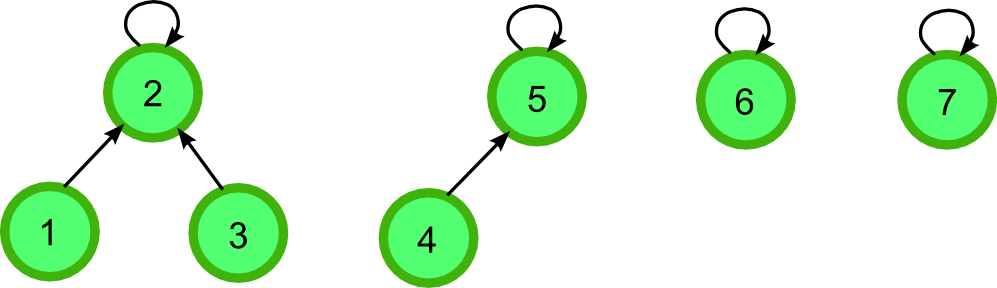
Заведём массив p, в котором для каждого элемента мы храним номер его предка в дереве:
int p[maxn];
for (int i = 0; i < n; i++)
p[i] = i;
Для запроса «в каком множестве элемент » нужно подняться по ссылкам до корня:
int leader(int v) {
if (p[v] == v)
return v;
else
return leader(p[v]);
}
Для объединения двух множеств нужно подвесить корень одного за корень другого:
void unite(int a, int b) {
a = leader(a), b = leader(b);
p[a] = b;
}
К несчастью, в худшем случае такая реализация работает за — можно построить «бамбук», подвешивая его раз за новую вершину. Сейчас мы это исправим.
#Оптимизации
Сначала привидем идеи оптимизации, а потом проанализируем, насколько хорошо они работают.
Эвристика сжатия пути. Оптимизируем работу функции leader. Давайте перед тем, как вернуть ответ, запишем его в p от текущей вершины, то есть переподвесим его за самую высокую.
int leader(int v) {
return (p[v] == v) ? v : p[v] = leader(p[v]);
}
Следующие две эвристики похожи по смыслу и стараются оптимизировать высоту дерева, выбирая оптимальный корень для переподвешивания.
Ранговая эвристика. Будем хранить для каждой вершины её ранг — высоту её поддерева. При объединении деревьев будем делать корнем нового дерева ту вершину, у которой ранг больше, и пересчитывать ранги (ранг у лидера должен увеличиться на единицу, если он совпадал с рангом другой вершины). Эта эвристика оптимизирует высоту дерева напрямую.
void unite(int a, int b) {
a = leader(a), b = leader(b);
if (h[a] > h[b])
swap(a, b);
h[b] = max(h[b], h[a] + 1);
p[a] = b;
}
Весовая эвристика. Будем вместо ранга хранить размеры поддеревьев для каждой вершины, а при объединении — подвешивать за более «тяжелую».
void unite(int a, int b) {
a = leader(a), b = leader(b);
if (s[a] > s[b])
swap(a, b);
s[b] += s[a];
p[a] = b;
}
Эвристики выбора вершины-лидера взаимоисключающие, но их можно использовать вместе со сжатием путей.
#Реализация
Финальная реализация, использующая весовую эвристику и эвристику сжатия путей:
int p[maxn], s[maxn];
int leader(int v) {
return (p[v] == v) ? v : p[v] = leader(p[v]);
}
void unite(int a, int b) {
a = leader(a), b = leader(b);
if (s[a] > s[b])
swap(a, b);
s[b] += s[a];
p[a] = b;
}
void init(n) {
for (int i = 0; i < n; i++)
p[i] = i, s[i] = 1;
}
Автор предпочитает именно весовую эвристику, потому что часто в задачах размеры компонент требуются сами по себе.
#Асимптотика
Эвристика сжатия путей улучшает асимптотику до в среднем. Здесь используется именно амортизированная оценка — понятно, что в худшем случае нужно будет сжимать весь бамбук за .
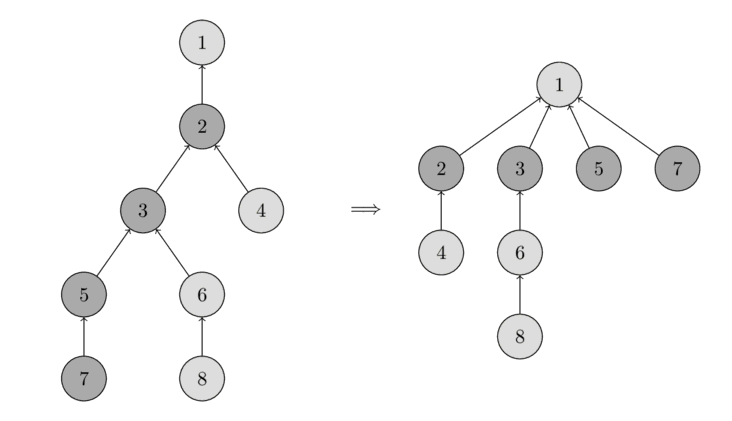
Индукцией несложно показать, что весовая и ранговая эвристики ограничивают высоту дерева до , а соответственно и асимптотику нахождения корня тоже.
При использовании эвристики сжатия плюс весовой или ранговой асимптотика будет , где — обратная функция Аккермана (очень медленно растущая функция, для всех адекватных чисел не превосходящая 4).
Тратить время на изучения доказательства или даже чтения статьи на Википедии про функцию Аккермана автор не рекомендует.