Суффиксный массив

Суффиксный массив, автомат и дерево обобщённо называют суффиксными структурами данных. Они применяются в множестве различных задач, встречающихся как на олимпиадах, так и на практике.

Суффиксные структуры часто (но не всегда) взаимозаменяемые, и более того, конвертируются друг в друга за линейное время. Суффиксный массив — самый простой из них, поэтому мы с него и начнём.

#Мотивация

Суффиксным массивом (англ. suffix array, суфмасс) строки $s$ называется перестановка индексов начал её суффиксов, которая задаёт порядок их лексикографической сортировки. Иными словами, чтобы его построить, нужно выполнить сортировку всех суффиксов заданной строки.

Где это может быть полезно. Пусть вы хотите основать ещё один поисковик, и чтобы получить финансирование, вам нужно сделать хоть что-то минимально работающее — хотя бы просто научиться искать по ключевому слову документы, включающие его, а также позиции их вхождения (в 90-е это был бы уже довольно сильный MVP). Простыми алгоритмами — полиномиальными хешами, z- и префикс-функцией и даже Ахо-Корасиком — это сделать быстро нельзя, потому что на каждый раз нужно проходиться по всем данным, а суффиксными структурами — можно.

В случае с суффиксным массивом можно сделать следующее: сконкатенировать все строки-документы с каким-нибудь внеалфавитным разделителем ($), построить по ним суффиксный массив, а дальше для каждого запроса искать бинарным поиском первый суффикс в суффиксном массиве, который меньше искомого слова, а также последний, который меньше. Все суффиксы между этими двумя будут включать искомую строку как префикс.

Например, строка iss в суффиксном массиве из примера найти будет зажата между суффиксами issippi$ и ississippi$, которые имеют индексы $2$ и $5$, а значит ровно на этих позициях и будет входить в исходный текст.

Работать такой алгоритм будет за $O(|t| \log |s|)$, и позже это можно будет оптимизировать до $O(|t| + \log |s|)$, что является одним из самых оптимальных алгоритмов поиска.

Теперь научимся его строить.

#Построение суффиксного массива

Для сортировки суффиксов мы могли бы просто взять перестановку от $0$ до $n$, написать компаратор, который сравнивает суффиксы с соответствующими индексами, и скормить это в std::sort, что будет работать за $O(n^2 \log n)$, потому что внутреннее сравнение работает за $O(n)$. Однако, если сравнивать суффиксы хешами, то уже можно получить алгоритм за $O(n \log^2 n)$. Но это не самый быстрый и удобный алгоритм.

#Построение за $O(n \log n)$

Для удобства допишем в конец строки какой-нибудь символ, который лексикографически меньше любого другого. Для стандартной ASCII обычно выбирают либо «$», либо «#», либо просто нулевой символ, если это C-string (в языке Си все строки и так заканчиваются нулевым символом).

Мы будем выполнять сортировку не суффиксов, а циклических сдвигов. Строки мы, соответственно, тоже будем рассматривать циклические — это удобно тем, что у них всех будет одна и та же длина. Легко убедиться, что сортировка таких циклических сдвигов эквивалентна сортировке суффиксов — можно просто убрать всё, что идёт после доллара.

Наш алгоритм будет состоять из $\lceil \log n \rceil$ этапов. На $k$-том этапе будем сортировать все циклические подстроки длины $2^k$. Так на последнем этапе мы отсортируем строки длины $\geq n$ (это легально — строки ведь циклические), и мы получим нужный суффиксный массив.

Заметим, что в отличие сортировки суффиксов, сортировка подстрок не всегда однозначна — две подстроки могут быть одинаковыми. Поэтому на каждой фазе алгоритма помимо перестановки $p$ индексов циклических подстрок будем поддерживать для каждой циклической подстроки номер её класса эквивалентности $c_i$, которому эта подстрока принадлежит. Номера классов эквивалентности будем давать с сохранением порядка: лексикографически меньшим подстрокам соответствуют меньшие $c_i$. После последнего этапа массив классов эквивалентности должен задавать перестановку, обратную суффиксному массиву.

Пример: $s = aaba$. Этапов будет 3: для подстрок длины 1, 2 и 4.

Как настоящие программисты, мы нумеруем этапы с нуля, поэтому на нулевом этапе мы отсортируем строки длины $2^0 = 1$, то есть просто символы. Если алфавит небольшой, то это легко сделать сортировкой подсчётом за $O(n)$.

Следующие этапы нужно проводить, используя информацию с предыдущих. Как в исходном решении, можем снова создать перестановку индексов и применить к ней std::sort со своим компаратором.

Для быстрого сравнения двух подстрок размера $2^{k-1}$ мы можем использовать классы эквивалентности $c_i$, сопоставив каждой строке длины $2^k$ биграмму — строку из двух «символов». А именно, строка $s[i \ldots i+2^k-1]$ с точки зрения сортировки будет эквивалентна паре $(c_i, c_{i+2^{k-1}})$. Соответственно, можно написать компаратор, который смотрит только на эти пары, и работает за $O(1)$ вместо линейного прохода по строкам. Однако, это всё ещё будет работать за $O(n \log^2 n)$, потому что каждый этап работает за $O(n \log n)$.

Примечание. Зачастую этот способ построения работает быстро, поскольку имеет небольшую константу.

Чтобы соптимизировать каждый этап до линейного, нужно избавиться от логарифма в сортировке. Сортировка слиянием оптимальна только тогда, когда мы ничего не знаем про сортируемые значения — но в нашем случае это не так.

Воспользуемся идеей цифровой сортировки — сначала отсортируем биграммы по второму символу, а потом по первому. С предыдущего этапа мы уже знаем порядок вторых элементов (это ровно массив $p$). Теперь, чтобы упорядочить их по первому, нам надо просто пройтись по суффиксам в этом порядке, от начала каждого элемента отнять $2^{k-1}$, чтобы получить индекс начала, и провести цифровую сортировку. Таким образом, можно проводить каждый этап за $O(n)$, а весь алгоритм за $O(n \log n)$.

// строка -- это последовательность чисел от 1 до размера алфавита
vector<int> suffix_array(vector<int> &s) {
    s.push_back(0);  // добавляем нулевой символ в конец строки
    int n = (int) s.size(),
        cnt = 0,  // вспомогательная переменная: счётчик для сортировки 
        cls = 0;  // количество классов эквивалентности
    vector<int> c(n), p(n);
    
    map<int, vector<int>> t;
    for (int i = 0; i < n; i++)
        t[s[i]].push_back(i);
    
    // «нулевой» этап
    for (auto &x : t) {
        for (int u : x.second)
            c[u] = cls, p[cnt++] = u;
        cls++;
    }
    
    // пока все суффиксы не стали уникальными
    for (int l = 1; cls < n; l++) {
        vector< vector<int> > a(cls);  // массив для сортировки подсчётом
        vector<int> _c(n);  // новые классы эквивалентности
        int d = (1 << l) / 2;
        int _cls = cnt = 0;  // новое количество классов
        
        for (int i = 0; i < n; i++) {
            int k = (p[i] - d + n) % n;
            a[c[k]].push_back(k);
        }
        
        for (int i = 0; i < cls; i++) {
            for (size_t j = 0; j < a[i].size(); j++) {
                // если суффикс начинает новый класс эквивалентности
                if (j == 0 || c[(a[i][j] + d) % n] != c[(a[i][j - 1] + d) % n])
                    _cls++;
                _c[a[i][j]] = _cls - 1;
                p[cnt++] = a[i][j];
            }
        }
        
        c = _c;
        cls = _cls;
    }
    
    return vector<int>(p.begin() + 1, p.end());
}

Автор извиняется за качество кода и призывает читателей его переписать и законтрибьютить.

#Наибольшие общие префиксы

Для многих применений часто бывает полезным возможность находить длину наибольшего общего префикса (англ. largest common prefix) для различных суффиксов строки.

Например, чтобы просто сравнить две подстроки, мы можем найти наибольший префикс соответствующих суффиксов и посмотреть на следующий символ — так же, как это обычно делается хешами.

Утверждение. Пусть мы знаем lcp для всех суффиксов, которые являются соседями в суффиксном массиве — это будет какой-то массив длины $(n - 1)$. Тогда общий префикс для $i$-того и $j$-того суффикса будет равен минимуму между $c_i$-тым и $c_j$-тым элементом в массиве lcp (напомним, что $c_i$ — класс эквивалентности — это номер $i$-того суффикса в суффиксном массиве).

Для доказательства можно представить массив lcp в виде гистограммы. Минимум на отрезке между $c_i$ и $c_j$ будет соответствовать суффиксу, который имеет самый короткий общий префикс с ними, а значит все символы до этого префикса и только они и будут наибольшим общим префиксом.

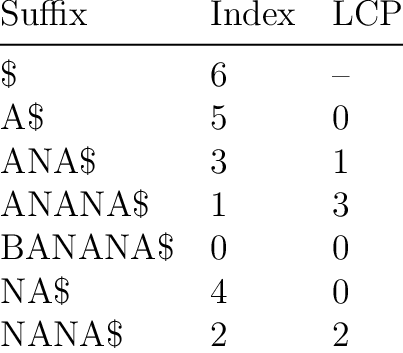
Тогда есть мотивация посчитать массив lcp$ в котором окажутся наибольшие общие префиксы соседних суффиксов, а после как-нибудь считать минимумы на отрезках в этом массиве (например, с помощью разреженной таблицы).

Осталось придумать способ быстро посчитать массив lcp. Можно воспользоваться идеей из построения суффиксного массива за $O(n \log^2 n)$: с помощью хешей и бинпоиска находить lcp для каждой пары соседей. Такой метод работает за $O(n \log n)$, но является не самым удобным и популярным.

#Алгоритм Касаи, Аримуры, Арикавы, Ли, Парка

Алгоритм в реальности называется как угодно, но не исходным способом (алгоритм Касаи, алгоритм пяти корейцев, и т. д.). Используется для подсчета $lcp$ за линейное время. Автору алгоритм кажется чем-то похожим на z-функцию по своей идее.

Утверждение. Пусть мы уже построили суфмасс и посчитали $lcp[i]$. Тогда:

По-русски: $lcp$ от следующего суффикса в исходной строке не более чем на единицу меньше.

Доказательство. Если для $p[i]$-го суффикса была общая часть длины $lcp[i]$ с $p[i + 1]$-ым суффиксом, то у $(p[i] + 1)$-го суффикса гарантированно будет общая часть длины $(lcp[i] - 1)$ с $(p[i + 1] + 1)$-ым суффиксом.

Заметим, что этот суффикс уже не обязательно будет соседом $(p[i] + 1)$-го в суффиксном массиве, но из свойства $lcp$ двух произвольных суффиксов получим, что $lcp[c[p[i] + 1]] \ge lcp[i] - 1$. Здесь возникает идея просто считать точное значение $lcp$ наивным образом — увеличиваем, пока увеличивается — но брать его стартовое значение, опираясь на это неравенство. В таком случае, чтобы не делать лишние сравнения, будем считать также считать массив $lcp$ в порядке от длинных суффиксов к коротким.

Код алгоритма:

    vector<int> calc_lcp(vector<int> &val, vector<int> &c, vector<int> &p) {
        int n = val.size();
        int l = 0; // lcp текущего элемента
        vector<int> lcp(n);
        for (int i = 0; i < n; i++) {
            if (c[i] == n - 1)
                continue;
            int nxt = p[c[i] + 1];
            while (max(i, nxt) + l < n && val[i + l] == val[nxt + l])
                l++;
            lcp[c[i]] = l;
            l = max(0, l - 1);
        }
        return lcp;
    }

Чтобы оценить сложность алгоритма, посчитаем, сколько раз мы сделаем наивное прибавление. Каждый $lcp[i] \le n$, а также мы сделаем не более $n$ вычитаний единицы при переходах. Тогда суммарное число прибавлений — $O(n)$. Следовательно, и сам алгоритм будет работать за $O(n)$.